Mix van aanpakken voor rekenen bij jonge kind
Ook onze Vlaamse collega’s zijn druk bezig met het herzien van hun onderwijsdoelen voor het funderend onderwijs. Zo deelde Pedro de Bruijkere op 30 april 2025 het artikel “What the Science of Learning Teaches Us About Arithmetic Fluency” (McNeil et al., 2025) als een recent voorbeeld voor hoe uit de cognitief psychologisch perspectief aangekeken wordt tegen het ontwikkelen van een reken-wiskundig repertoire van het jonge kind.
Het zou moeten gaan om een combinatie van stampen en begrijpen volgens Pedro. De auteurs noemen het een combinatie van memoriseren en denkstrategieen.
Het artikel is een uitgebreid overzicht van wetenschappelijk onderzoek naar rekenvaardigheid (met name vlotheid in elementaire basisbewerkingen) en hoe die het best ontwikkeld kan worden. In het artikel staat een grote rijkdom aan bronnen en benaderingen genoemd. Hert zou een mooi startpunt zijn voor een open en constructieve discussie over verschillende visies op hoe jonge kinderen zich ontwikkelen in het domein van rekenen-wiskunde. De auteurs proberen een brug te slaan naar andere perspectieven, maar komen helaas ook zelf weer snel terecht in de valkuil van – met enige arrogantie – het eigen cognitief-psychologische perspectief als superieur te beschouwen als “THE science of learning”, met beleefde diskwalificatie of misrepresentatie van andere perspectieven (“Is allemaal zelf ontdekken en dat kan niet bij aanvankelijk rekenen”).
Dat is misschien ook wel een probleem van de huidige tijd. Er lijkt een sterke bubbelwerking te zijn. De auteurs lijken een blinde vlek te hebben voor wat er de afgelopen 60 jaar is gepubliceerd over aanvankelijk rekenonderwijs in het corpus van vakdidactisch, en dus domeinspecifiek, onderwijsonderzoek naar aanvankelijk reken- en wiskundeonderwijs.
Begrippen als horizontaal en verticaal mathematiseren, ‘guided reinvention’, ‘numeracy as a social practice’, en mathematiseren van probleemsituaties ontbreekt geheel in het artikel. Ik noem een paar auteurs die daar tientallen artikelen en “seminal” boeken over hebben geschreven: Saracho, Spodek, Kaminski, Dehaene, Lave & Wenger, Van den Heuvel-Panhuijzen, Skemp, en nog vele anderen. Die komen allemaal niet voor in de referenties.
Er komt een nogal technocratisch beeld uit het artikel naar voren alsof kinderen gereduceerd worden tot een soort informatieverwerkingsunits zijn, waarbij het vooral gaat of de juiste input op het juiste moment en met de juiste snelheid de juiste output levert. Aangezien dit ook het leidende beginsel is van het Westerse naoorlogse onderwijsmodel paste dat goed op elkaar en is daar veel onderzoek naar gedaan worden en gekeken hoe die output – vrijwel uitsluitend op toetsen of op post-tests – steeds een beetje verbeterd kan worden. Daarom ook die voorspellende waarde van het geleerde op steeds weer vergelijkbare schoolgebonden toetsen verderop in de loopbaan. Vergelijk het met het steeds verder incrementeel verbeteren van de benzineauto.
Het is natuurlijk ook een gegeven dat daarbij ook heel veel leerlingen uitvielen, rekenangst of vergelijkbare trauma’s ontwikkelden, en uiteindelijk een zeer plat, niet functioneel repertoire overhielden als het gaat om het omgaan met getallen in hun wereld. De auteurs bespreken wel een aantal problemen die dit in het verleden hebben opgeleverd, zoals de bekende gerichtheid op alleen maar gehele getallen, fixatie op louter het uitrekenen van het goede antwoord, ‘suspension of sensemaking’, hetgeen het best te vertalen is als ‘het verstand op nul zetten’ en gewoon nadoen.
Ook de nadruk op de term memoriseren verwart mij wat. Mogelijk dat er allemaal nuances zijn in de definitie wat memoriseren, maar meer passend bij wat je met deze kinderen wilt bereiken is internaliseren. Dat is een belangrijk en veel rijker psychologisch begrip en dat zo maar reduceren tot memoriseren is te plat. Het memoriseren dat bij 7 x 8 het getal 56 hoort is in mijn ogen geen wiskundig denken, maar louter een geheugenoefening. Bij 7 x 8 – zo of in een andere representatie – zouden associaties en beelden moeten opkomen van een rijk associatief schema, waar 56 ook in thuishoort, met daarbij weten wanneer die 56 eigenlijk relevant is.
Voorbeeldje: Het wiskundige 6 x 4 is natuurlijk veel meer dan alleen een gememoriseerde 24. Het staat voor een vermenigvuldigstructuur die allerlei betekenissen kan hebben: herhaald optellen, ordenen in kratjes, 6 stuks van 4 elk., et cetera. Daar zou uitgebreid aandacht voor moeten zijn tijdens het ontwikkelen van de uitrekenvaardigheid. Dan ben je een rijk wiskundig denkschema aan het internaliseren.
De auteurs tonen ook een weinig doorontwikkelde visie op wat hedendaags steeds belangrijker is geworden bij rekenen-wiskunde in een veranderende wereld. We rekenen echt veel minder uit dan vroeger, de meeste berekeningen zijn in apparaten, software en apps verdwenen. Het met pen en papier uitvoeren van grote bewerkingen is wereldwijd uit het menselijk handelen verdwenen.
___________________________________________________________________________________________________________________________________________________________
Het met pen en papier uitvoeren van grote bewerkingen is wereldwijd uit het menselijk handelen verdwenen.
____________________________________________________________________________________________________________________________________________________________
Dit maakt het noodzakelijk om ook een nieuwe blik te werpen op hoe het aanleren van die aanvankelijke rekenfeiten het best kan gebeuren. Het gaat tegenwoordig in toenemende mate ook om het interpreteren van getallen, daarmee redeneren, daarmee uit het hoofd schattingen maken. Verder wordt steeds belangrijkern om gewend te raken aan de grote diversiteit van hoe getallen tegenwoordig worden gebruikt en gerepresenteerd. En daar zou je zeker op de betreffende leeftijd aandacht moeten besteden. Die ervaringen mag je leerlingen niet onthouden door bijvoorbeeld alleen maar schoolse oefenblaadjes door te werken. De veranderende wereld vraagt erom dat de input aan kinderen meer multimodaal en multimodaal is.
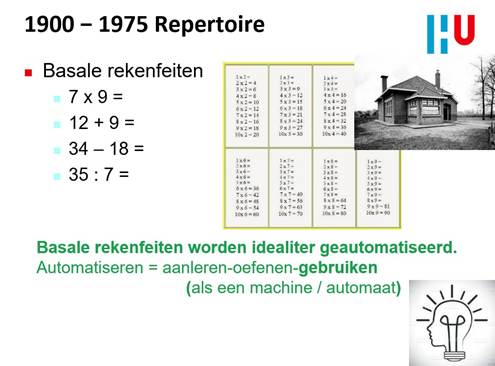
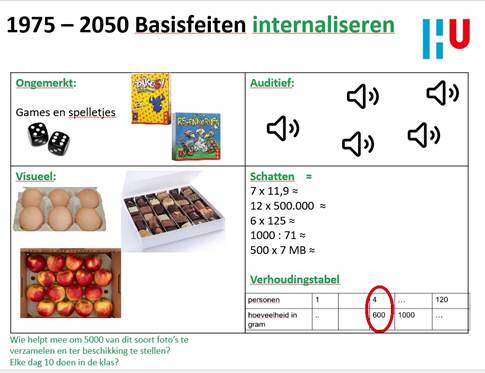
En dat er rekening gehouden wordt met hogere orde vaardigheden en de affectieve componenten van hoe de leerling zich op zijn/haar niveau verhoudt tot dat idealiter rijke onderwijsaanbod van de leraar. En ja, daarover zijn natuurlijk geen randomized controlled trials te vinden 10, 20, 30 of 50 jaar geleden. Het lijkt meer op in het hier en nu te ontwikkelen in proeftuintjes wat er nodig is om een goede elektrische auto’s te maken.
De uiteindelijke aanbevelingen van de auteurs zijn ronduit teleurstellend te noemen.
Table 2.
Practice Recommendations for Building Arithmetic Fluency.
1. Monitor and ensure that early knowledge of numbers, relations, and operations are forming on the path toward arithmetic fluency.
2. Provide explicit instruction to clearly and directly teach important strategies and concepts.
3. Implement well-structured retrieval practice to reinforce learning and build a robust, interconnected memory network.
4. Introduce time-limited practice only after students demonstrate accuracy in their responses.
5. Allocate sufficient time for comparing different representations and strategies, discussion, and reflection.
Het is gewoon het voortdurend terugkerend standaardrijtje van de huidige cognitief onderwijspsychologen: instructie, herhalen, oefenen onder druk. Met aan het eind van het proces nog wat reflectie op strategieën, wat dan blijkbaar de aangekondigde denkstrategieën zijn.
Mogelijk interessante extra informatie
In Nederland verscheen in april jongstleden De Staat van het Onderwijs 2025. Daarin was interessant hoe beschreven werd wat leraren in Nederland zoal in de klas doen:
Bij rekenen-wiskunde: meer aandacht voor probleemoplossen nodig
Het didactisch handelen van de leraar doet ertoe: het draagt bij aan de ontwikkeling van leerlingen. Het directe instructiemodel waarbij de leraar via onder andere expliciete uitleg en door voor- en nadoen rekenkennis en -vaardigheden overdraagt, is bij rekenen wiskunde in het po en so de meest gangbare instructie-aanpak. Daarnaast zeggen de meeste leraren aandacht te hebben voor de toepassing van het geleerde in en transfer naar andere (betekenisvolle) situaties, waarbij leerlingen zelf actief moeten nadenken.
Ongeveer driekwart van de po-leraren zegt alle of bijna alle rekenlessen volgens het directe instructiemodel te geven. Ontdekkend en onderzoekend leren waarbij leerlingen via onderzoeken en ontdekken tot leren komen, komt minder vaak voor. De meerderheid van leraren geeft aan deze vorm van leren in sommige rekenlessen in te zetten (bo: 70%; sbo: 60%; so: 57%). De sturing in de rekenlessen ligt veelal bij de leraren. Ongeveer de helft van de sbo- en so-leraren en bijna 70% van de bo-leraren laat leerlingen elke rekenles zelfstandig oefenen met het toepassen van het geleerde in nieuwe probleemsituaties (Inspectie van het Onderwijs, 2024j). Dit laatste kunnen leraren nog vaker doen zodat leerlingen (meer) oefening krijgen in het zelfstandig oplossen van problemen in nieuwe situaties. Het zogeheten wiskundig probleemoplossen is namelijk de lastigste categorie opgaven voor leerlingen (zie ook paragraaf 2.2). Deze gaat over de vaardigheid om wiskundige problemen te formuleren, te representeren en op te lossen, terwijl niet direct duidelijk is hoe de oplossing kan worden gevonden. (De Staat van het Onderwijs 2025, p.42)
Dit is ook weer niet zo verschillend van wat er in het artikel wordt aangeraden. Alleen doen deze leraren het in het echt en niet vanuit een top-down framework. Mogelijk ook een verklaring waarom Nederland al 25 jaar ver boven het gemiddelde scoort bij rekenen in alle internationale ranglijsten (TIMSS, PISA en PIAAC).
Ontwikkeling van reken-wiskundig denken van jonge kind
In eerdere nummers van Volgens Bartjens (38-4 , 38-5, 39-1, 39-2, 39-3 , blog1, blog2) heb ik al enkele onderzoeken aangehaald die betrekking hadden op de ontwikkeling van reken-wiskundig denken van het jonge kind.
Eentje over de rol die ICT hierbij zou kunnen spelen als er gekozen wordt voor een heel speelse benadering (38-4). En eentje hoe het werken aan patronen en ruimtelijk figuren een positief effect heeft op het latere schoolsucces bij rekenen en wiskunde (38-4). En eentje die het positieve effect heeft gemeten van het gebruik van Building Blocks door jonge kinderen (38-5)
