Cognitieve psychologie en rekenontwikkeling jonge kind: een te beperkt model.

The Science of Learning

Eind april 2025 verschijnt er een zeer intrigerend artikel “What the Science of Learning Teaches Us About Arithmetic Fluency” in het tijdschrift Psychological Science in the Public Interest. Het beslaat niet minder dan 38 bladzijden, waarvan 9 met referenties. Het gaat vooral om aanvankelijk rekenonderwijs en wat de rol van “arithmetical fluency” daarin zou moeten zijn.

Daarmee is het onderwerp zeer actueel in de discussies die momenteel in allerlei landen worden gevoerd over de inrichting van het reken-wiskundeonderwijs binnen het funderend onderwijs (leeftijd 4-16) en de rol van het oefenen met kale bewerkingen daarin, voorschools, op school en naschools.

Definitie van “arithmetical fluency”

De beginzin zet direct de toon: “Arithmetic proficiency is a powerful tool for making everyday decisions, achieving academic and professional success, and improving our world. “ (p.10)

Ik zie de meeste van de artikelen over reken- en wiskundeonderwijs gewoonlijk beginnen met:  Mathematics is a powerful tool ….

De in dit artikel gehanteerde definitie van “arithmetic fluency” luidt: “Arithmetic fluency is the efficient, accurate, and relatively effortless mental production of sums and products of the numbers 0 through 10 (and their inverses) when given their associated number combinations and vice versa.” (p.11)

Het lijkt dus te gaan om één heel specifieke set van getalsmatige bewerkingen

• Van de soort “ééncijferig getal bewerking ééncijferig getal is ….,”
• Genoteerd in een vaste –  wiskundig meest formele –  vorm 4 x 7 = …
• Gericht op het invullen van het juiste getal op de puntjes.
• Binnen 2 seconden

De toevoeging “vice versa” lijkt er op te duiden dat de hele set gaat om de volgende formele sommetjes:

Het artikel betoogt dat in de cognitief psychologisch onderzoek precies deze set – precies in deze vorm – het fundament is om leerlingen een succesvol repertoire van rekenwiskundig denken en handelen bij te brengen en dat de resultaten op dergelijke sommen een voorspellende waarde hebben voor later schoolsucces, zeker bij de STEM-vakken.

Er zijn natuurlijk andere perspectieven op hoe bij jonge kinderen een fundamenteel cognitief schema rond getallen en bewerkingen zich ontwikkelt en met welk type onderwijs dat schema kan uitgroeien tot een bruikbaar en flexibel in te zetten repertoire en tegelijk gewerkt wordt aan een introductie in de conceptuele – begripsgestuurde – wereld van rekenen-wiskunde. Die andere perspectieven komen voornamelijk voort uit zo’n 70 jaar domeinspecifiek onderzoek naar rekenen-wiskundeonderwijs, ook wel vakdidactisch onderzoek genoemd. Math Education Research wordt wereldwijd gezien als een erkend zelfstandig onderzoeksgebied met een zeer groot en divers corpus aan wetenschappelijk onderzoek. De conferenties ICME (4 jaarlijks wereldwijd, meer dan 100 landen), CERME (2 jaarlijks, vooral Europees) en PME (jaarlijks, wereldwijd) zijn daarin conceptueel toonaangevend.  Vanuit die wetenschappelijke kennisbasis wordt over het algemeen een breder, meer holistisch en meer multidisciplinair perspectief geboden op de cognitieve schema’s die leerlingen ontwikkelen op het gebied van rekenen-wiskunde en waar ze in hun verder schoolloopbaan gebruik van maken (wiskunde, statistiek), maar zeker ook in het dagelijkse leven (gecijferdheid). De schema’s zijn ook nodig om volwaardig te kunnen participeren in onze steeds verder “mathematiserende” samenleving. Onderstaand raamwerk dat de afgelopen jaren is ontwikkeld geeft dat bredere perspectief weer.

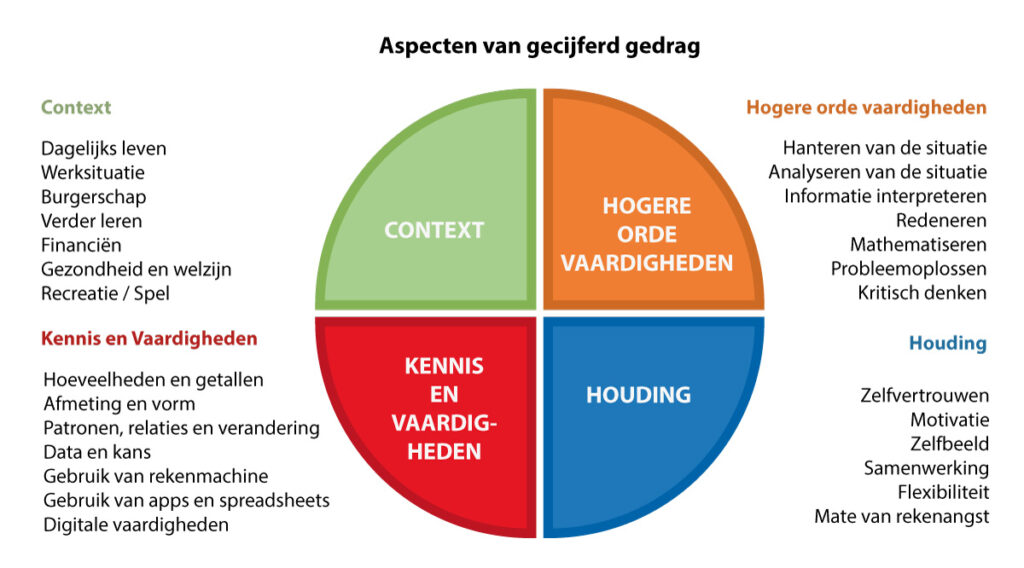
Common European Numeracy Framework (cenf.eu)

Wat dat betekent voor bijvoorbeeld een passende set basisfeiten, wordt verderop geconcretiseerd.

Reken-wiskundeonderwijs op school speelt uiteraard een belangrijke rol bij het ontwikkelen van die bredere schema’s die een verbinding slaan tussen concrete ervaringen van leerlingen en meer formele notaties die gebruikelijk zijn in ons getalstelsel en het positiestelsel daarbinnen.  

Die holistische aard toont zich ook bijvoorbeeld in het besef dat de individuele wiskundige cognitieve schema’s van leerlingen zich al beginnen te vormen vrijwel direct na de geboorte en dat deze worden uitgebreid, verrijkt en verfijnd door nieuwe ervaringen, bedoeld of onbedoeld, gepland en ongepland in veel verschillende vormen – de wereld is nu eenmaal veelvormig.

Cruciale keuzes

De auteurs van het artikel vernauwen de discussie vanuit de verschillende perspectieven  tot de volgende twee  vragen:

1. Leer je “arithmetic fluency”  het beste door memorization of door thinking strategies?
2. Maakt de aanwezigheid van rekenmachines het aanleren van “arithmetical fluency” nog relevant?

Het zijn typisch het soort vragen die in het publieke debat over rekenen een rol spelen. Voor cognitief psychologen voor wie de werking van het geheugen centraal staat in hun leertheorie zijn deze vragen een no-brainer: (1) memoriseren en (2) ja, en verbied het gebruik van de rekenmachine zo lang mogelijk.

Een vakdidactisch onderzoeker echter zal meer waarschijnlijk opmerken dat de hier gepresenteerde basisset eendimensionaal en abstract is en eerder het eind van een leerlijn is dan een fundament – na tal van didactische verkortingen in de route van ervaringen in de werkelijkheid naar de taal en abstractie van wiskunde. Dat in het hoofd van leerlingen vrijwel zeker cognitieve schema’s in ontwikkeling zijn die een veel multimodalere vorm hebben dan deze basisset in deze vorm. En dat op dat fundament verder gebouwd moet kunnen worden in de richting van een functioneel en met de realiteit verbonden repertoire van productieve wiskundige denk- en handelwijzen. Daarbij horen ook hogere orde doelen als redeneren, mathematiseren en probleem-oplossen. Deze staan ook in vrijwel elke landelijke curriculumbeschrijving ter wereld als doelen van het hedendaagse reken-wiskundeonderwijs.

De vraag blijft waarom die heel beperkte set die in dit artikel gepropageerd wordt, zo’n dominante plaats heeft in ons collectieve geheugen.

Dat vereist mogelijk enige uitleg en detaillering.  Zo’n basisset krijgt algemene waarde als deze veel gebruikt wordt, liefst heel veel en niet alleen in de lessen waarin de set wordt aangeleerd, en niet alleen op de volgende toets, en niet alleen in de bèta-schoolvakken die er mogelijk de tien jaar daarna nog op volgen.

In het onderwijs van de vorige eeuw, zeker tot 1975, was de enige manier om complexere berekeningen als

 1.236 + 98.345 = …

646 x 27 = …

17.000 – 8.430 = … 

116.331 : 17 = …

uit te rekenen door middel van het inzetten van – al dan niet gestandaardiseerde – algoritmen.

De staartdeling is hiervan het icoon geworden.

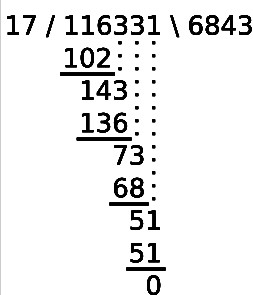
Voor het uitvoeren van deze algoritmen waren die formele rijtjes van de hier genoemde basisset, specifiek in deze uitrekenvorm, een handige onderlegger. Kortom de ééndimensionale opvatting over “arithmetical fluency” was in de periode voor 1975 consistent met heel veel van het dagelijkse  handelen op het gebied van vooral uitrekenen. Het verder toepassen of gebruiken om problemen uit het echte leven te mathematiseren en op te lossen schoot daarbij in. Onderwijstijd was en is uiteindelijk beperkt.

In de periode na 1975 veranderde de aard van het reken-wiskundig handelen vrij radicaal. Het automatiseren van grote berekeningen verschoof, net als op talloze andere terreinen, van de mens naar de machine. De onderstaande plaatjes geven die transitie weer.

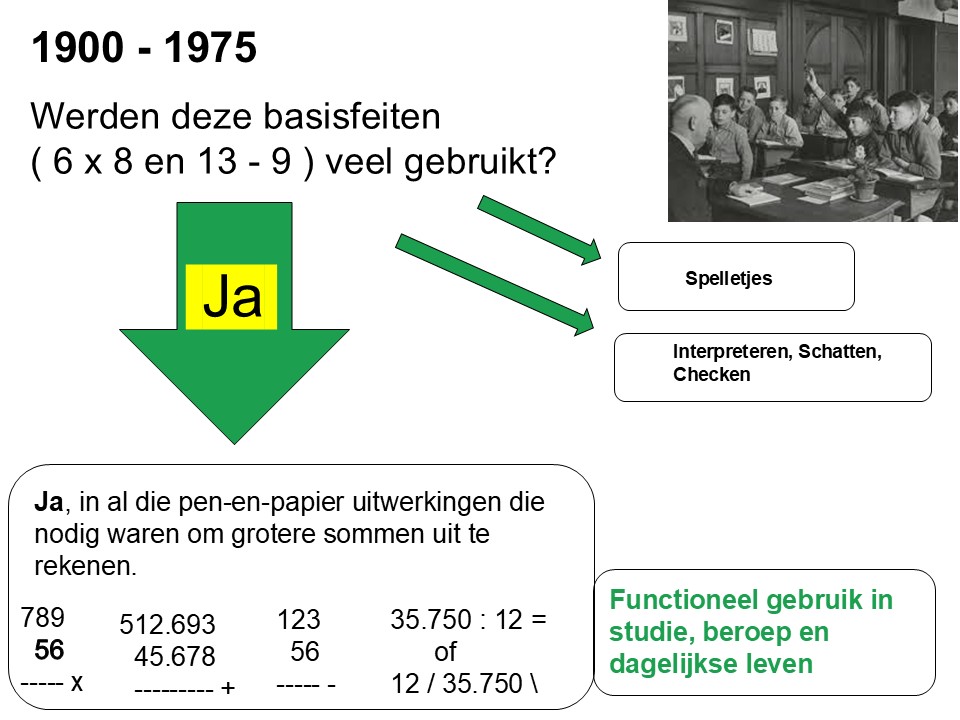
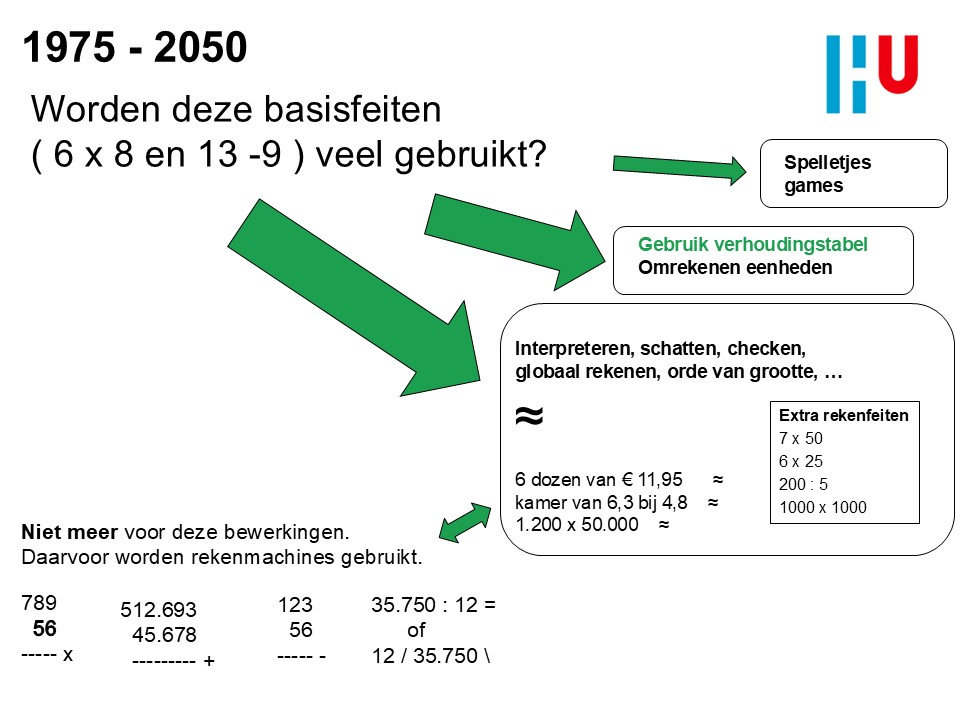
Laten we er geen doekjes om winden: het met pen en papier uitvoeren van grote bewerkingen is wereldwijd vrijwel uit het menselijk handelen verdwenen.

_______________________________________________________________________________________________________________________________________________________

Het met pen en papier uitvoeren van grote bewerkingen is wereldwijd uit het menselijk handelen verdwenen.

________________________________________________________________________________________________________________________________________________________

De elementaire basisfeiten moeten idealiter geïnternaliseerd worden in de individuele cognitieve schema’s van de leerlingen, maar bij het doen van grotere bewerkingen is de inzet van de rekenmachine handig, voor veel leerlingen een opluchting en ook nog affectief en motivationeel relevant omdat deze leerlingen dan verlost worden van steeds maar afgerekend worden op pen-en-papier werkwijzen die ze verder nooit gaan gebruiken. Leren de rekenmachine goed te gebruiken bij grote berekeningen schept ook de mogelijkheid en ruimte om aan andere doelen van reken-wiskundeonderwijs te werken. Enerzijds aan hogere orde doelen als redeneren met getallen, probleem oplossen, mathematiseren, kritisch beschouwen van getalsmatige informatie en de rekenmachine goed leren gebruiken: op het juiste moment in geschikte situaties. Ook geeft het de mogelijkheid om meer inclusief te werken, omdat er minder kinderen uitvallen, wanneer ze de vrij technische en hier en daar trucmatige algoritmen moeilijk of niet onder de knie kunnen krijgen.

Die ontwikkeling naar functioneel inzetten van de rekenmachine gaat echter heel erg langzaam. Het beeld dat rekenen eigenlijk nog steeds alleen maar het uitrekenen van makkelijke en moeilijke sommen is met pen en papier is zeer hardnekkig. Niet alleen door de collectieve ervaringen van voor 1975, maar ook uit sentiment en uit onwetendheid bij groot publiek wat je tegenwoordig feitelijk  dagelijks doet aan reken-wiskundig denken en handelen.

We zien dat in het mediadebat, vanuit politiek en beleidsmakers, maar ook vanuit veel wetenschappers – uit andere disciplines, die “rekenen” nemen als object van studie – dezelfde smalle en gedateerde beelden hergebruikt worden.

Geheugenonderzoekers die uitgaan van de genoemde beperkte set staan in het algemeen zeer afwijzend tegenover het gebruiken van een rekenmachine. De angst lijkt te zijn dat met een rekenmachine in de hand de zo belangrijke basisset geheel zou verkruimelen. Ook zijn er over de benodigde – aan de huidige tijd aangepaste – benaderingen natuurlijk geen randomized controlled trials te vinden van 10, 20, 30 of 50 jaar geleden.

De eerlijkheid gebiedt mij te zeggen dat aan de andere kant van het spectrum aan perspectieven ook doorgeschoten uitspraken gebezigd worden, zoals: “Kinderen hoeven niet meer leren rekenen, omdat er nu eenmaal rekenmachines zijn”. Zulke uitspraken zijn ook veel te kort door de bocht en volstrekt niet behulpzaam in de discussie. Ook dit zijn uitspraken van leken op het gebied van rekenwiskundedidactiek. De verbreding van de doelen vraagt juist meer en beter reken-wiskundeonderwijs door meer vakdidactisch opgeleide of nageschoolde leraren.

Ook vanuit het vakdidactisch perspectief speelt een individueel opgebouwd cognitief schema zich af in het hoofd, soms ondersteund door een flinke dosis ‘embodiment’

En, ja, een set basisfeiten voor bewerkingen die de leerlingen uit het hoofd paraat heeft, is daar een onlosmakelijk onderdeel van. Dat kan niet via een extern apparaat en extern geheugen geregeld worden. En, ja, de in het artikel genoemde basisset van de cognitief psychologen heeft daar overlap mee, niet in die rigide vorm, maar ingebed in een veel rijker schema. En hoogstwaarschijnlijk niet voor alle leerlingen verkort tot de meest abstracte en gedecontextualiseerde vorm. Onderstaande plaatjes geven daarvan een indruk.

Wat is tegenwoordig nodig aan wiskundige denk- en handelwijzen

De auteurs tonen ook een weinig doorontwikkelde visie op wat hedendaags steeds belangrijker is geworden bij het alledaags rekenwiskundig handelen en denken in een veranderende wereld. Het daadwerkelijk zaken moeten uitrekenen zonder gereedschap, is echt veel minder voorkomend dan vroeger, de meeste berekeningen zijn in apparaten, software en apps verdwenen.

Het gaat tegenwoordig in toenemende mate ook om het interpreteren van getallen, daarmee redeneren, daarmee uit het hoofd schattingen maken. Verder wordt steeds belangrijker om gewend te raken aan de grote diversiteit aan representaties van getallen. En daaraan zou je zeker bij de ontwikkeling van het jonge kind aandacht aan moeten besteden; het is de wereld waarin ze leven. Die ervaringen mag je leerlingen niet onthouden door bijvoorbeeld alleen maar schoolse oefenblaadjes met sommen in één vorm door te werken. De veranderende wereld vraagt erom dat de input aan kinderen meer multimodaal is: een soort “interpretational fluency”.

_______________________________________________________________________________________________________________________________________________________________

Die ervaringen mag je leerlingen niet onthouden door bijvoorbeeld alleen maar schoolse oefenblaadjes met sommen in één vorm door te werken. De veranderende wereld vraagt erom dat de input aan kinderen meer multimodaal is.

_______________________________________________________________________________________________________________________________________________________________

De auteurs beschrijven wel heel uitvoerig hoe kinderen natuurlijk al voor de schoolleeftijd allerlei ervaringen opdoen in de wiskundige wereld. Aantallen, 2D, 3D, proportioneel denken zijn allemaal zaken die vanzelf al voorbij zijn gekomen in het leven van de kinderen, wel heel verschillend en in verschillende mate van rijkheid, helaas ook afhankelijk van SES en “opportunities to learn”. De genoemde “early milestones” in het artikel zijn ook interessant en zinnig.

School voegt daar conventies, notaties en nieuwe inzichten aan toe en dat moet dan leiden tot een veel rijker individueel cognitief schema rond de belangrijkste en bekende wiskundige begrippen, denk- en handelwijzen. En dan na de schoolse periode van formeel onderwijs gaan ze daar dan weer mee verder in het dagelijkse leven als burger en als w

kende professional.  De genoemde beperkte formele basisset is in die cyclus toch een beetje een tussengepropt vreemd element: gedecontextualiseerd, ontdaan van betekenis, bedoeld om te memoriseren, omdat dat dat goed voor later is en blijkbaar niet primair om te gebruiken.

Wat is de waarde van het onderliggende onderzoek?

De auteurs zijn van mening dat:

“Although we cannot directly observe the internal representation of an arithmetic fact, or the cognitive steps taken to produce a sum or product, psychologists use models, clever experimental designs, and sophisticated methodological tools to draw informed inferences about the cognitive structures and processes involved in arithmetic fluency.”(p.12)

Deze zelffelicitatie lijkt mij wat overdreven. Ik vind in het vakdidactisch onderzoek de designs meer gebruik maken van verschillende methodologieën, van creatievere designs, en van een veel genuanceerdere doordenking van hoe het jonge kind de wereld van reken-wiskunde binnentreedt of door volwassenen wordt binnengeleid. Ik denk dan aan concepten als geleide herontdekking, progressieve schematisering (verkorten), horizontaal en verticaal mathematiseren, et cetera.  Ik zie dat soort concepten niet terug. Ik noem een paar auteurs die daar tientallen artikelen en “seminal” boeken over hebben geschreven: Saracho, Spodek, Kaminski, Dehaene, Lave & Wenger,  Van den Heuvel-Panhuijzen, Skemp, en nog vele anderen. Die komen allemaal niet voor in de referenties, noch een verwijzing naar een wereldwijde ICMI Study 23: Building the foundation: Whole Numbers in the Primary Grades.

Ook mis ik noties over het gebruik van het repertoire in andere situaties dan de reken-wiskundeles, zoals ‘numeracy as a social practice’, en ‘mathematiseren van probleemsituaties’ als cruciale concepten om te komen tot een bruikbaar en inzetbaar individueel repertoire in het leven van alledag. De literatuurlijst is zeer uitgebreid, maar wel vrijwel geheel vanuit één perspectief. Als dat wordt gevoeld als het meest waardevolle perspectief, dan is het artikel zeer overtuigend.

Onderliggend mensbeeld

De hier gepresenteerde basisset is gericht op procedures, gericht op goede antwoorden, gericht op reproduceren onder tijdsdruk. Aangezien dit ook het leidende beginsel is van het Westerse naoorlogse onderwijsmodel en van de industriële inrichting van heel veel van ons onderwijs, past dat goed op elkaar. Er is veel onderzoek gedaan binnen die schoolse context hoe die output – vrijwel uitsluitend op toetsen of op post-tests – steeds een beetje verbeterd kan worden.  Daarom ook die voorspellende waarde van het geleerde op steeds weer vergelijkbare schoolgebonden toetsen verderop in de loopbaan.

Negatieve gevolgen

Het is natuurlijk ook een gegeven dat bij de smalle benadering veel leerlingen uitvielen, rekenangst of vergelijkbare trauma’s ontwikkelden, en uiteindelijk een zeer plat, niet functioneel repertoire overhielden als het gaat om het omgaan met getallen in hun wereld. De paragraaf “common pitfalls” is interessant omdat daar concepten worden behandeld die al decennia ook in vakdidactisch onderzoek worden genoemd als problematisch en een reden om een nadere benadering te kiezen.

• Whole number bias: denken dat de wereld alleen maar draait om gehele getallen en berekeningen daartussen. De meeste getallen die we tegenkomen zijn dat niet, zoals huisnummers, serienummers, meetwaarden, etc.
• Operational view of math problems: denken dat het bij rekenen-wiskunde alleen gaat om het juiste antwoord, bijvoorbeeld dat bij het zien van 4 x 6 de reflex moet zijn om 24 te roepen. Terwijl de adequate reactie moet zijn: Welk probleem zijn we hiermee aan het oplossen? Wat wil je van mij met dit sommetje? Of is het wel een sommetje of gewoon de afmeting van de gewenste afdruk van de foto en waarom wil je dan dat ik 24 roep?
• Suspension of sense-making: het gevoel dat het gaat om het antwoord dat de leraar of het schoolboek of het digitale oefenprogramma wil horen en niet om iets echts. Dat het maar beter is om bij rekenwiskunde je verstand op nul te zetten en gewoon na te doen wat er van je gevraagd wordt.

Merkwaardigerwijs zijn dit nu juist de valkuilen die eigenlijk altijd genoemd worden als de cognitief psychologische benadering in de klas heeft geleid tot voortdurend oefenen zonder nadenken en voortdurend een beroep doen op geheugen in plaats van op snel en flexibel wiskundig denken, gevoed door een rijk individueel cognitieve schema.

De generieke aanbevelingen

De  uiteindelijke aanbevelingen van de auteurs zijn ronduit teleurstellend te noemen. Ik neem ze hieronder onvertaald op.

Practice Recommendations for Building Arithmetic Fluency.

1. Monitor and ensure that early knowledge of numbers, relations, and operations are forming on the path toward arithmetic fluency.

2. Provide explicit instruction to clearly and directly teach important strategies and concepts.

3. Implement well-structured retrieval practice to reinforce learning and build a robust, interconnected memory network.

4. Introduce time-limited practice only after students demonstrate accuracy in their responses.

5. Allocate sufficient time for comparing different representations and strategies, discussion, and reflection.

Dit is gewoon het voortdurend terugkerend generieke standaardrijtje van de huidige cognitief onderwijspsychologen: instructie, herhalen, oefenen onder tijdsdruk.  Met aan het eind van het proces nog wat reflectie op strategieën, wat dan blijkbaar de aangekondigde denkstrategieën zijn.

Persoonlijke reflectie

De eendimensionaliteit van de set en de eendimensionaliteit van het geheugen als primair vehikel zijn de zwakte van dit leertheoretisch model om echt te komen tot een grote kwaliteitsverbetering in het rekenwiskundeonderwijs. Desondanks kan het in de praktijk van de scholen een aantrekkingskracht hebben omdat het simpel via instructie te onderwijzen is en simpel te toetsen.

Wat me het meeste zorgen baart over de “strijd” tussen deze perspectieven is dat de polarisatie die optreedt een verlammend effect kan hebben. Dat de polarisatie kan leiden tot volkomen doorgeschoten wederzijdse karikaturen.

Ik denk dat het vooral een verschil in paradigma is hoe je tegen leren en de ontwikkeling van kinderen aankijkt. Ik vind het hier getoonde cognitief psychologisch perspectief nogal industrieel en schools: Input; output, instructie, reproductie op schoolse toetsen.
Ik vind de domeinspecifieke benadering – vanuit vakdidactiek rekenen wiskunde – holistischer, completer en meerdimensionaal. Onderwijs is sociale interactie tussen volwassene en kind vanuit kennis over leer- en ontwikkelingslijnen èn hoe het geleerde gebruikt wordt in de wereld.

In de praktijk in veel landen zie ik daarnaast dat het memoriseren en oefenen heeft geleid tot eindeloze batterijen toetsen om leerlingen, leraren, scholen zelfs hele landen af te rekenen, namelijk op het aantal goed of fout scores op tamelijk onzinnige kleine sommetjes of kleine eendimensionale contextopgaven. Ik ken eigenlijk geen voorbeelden van landen die de werkwijze zoals in dit artikel gepropageerd wordt, hebben geïmplementeerd bij rekenen-wiskunde en er toen opeens heel erg mee vooruit gingen. Ik ben in heel veel scholen in allerlei landen geweest en daar hielp het opdreunen van tafels weinig om het peil van het reken-wiskundeonderwijs te verhogen. Je zou zelfs kunnen zeggen dat een beleid als No Child Left Behind in de USA, met vrijwel letterlijk dezelfde narratieven als van de cognitief psychologen nu, eerder heeft geleid tot daling van het landelijke onderwijsniveau. Ik denk dat het model waarin je onderwijs inclusief, betekenisvol, niet gericht op selectie maar op het ontwikkelen van een individueel rijk cognitief schema nog steeds de beste kans maakt.

Nederland scoort bij PISA en TIMSS bij rekenen-wiskunde ver boven het OECD gemiddelde, behoort tot de top van Europa wat betreft resultaten en ziet in de lessen al decennialang een mix van instructie, oefenen, en werken aan contextrijke problemen. Dat laatste vinden leraren het lastigste en daar is ook de vraag het grootst naar verdere professionalisering.

Waarom zou je als basisschool in een land in Nederland je gaan richten op meer directe instructie, meer oefenen en jezelf moedwillig beperken tot een eendimensionale en abstracte benadering van een belangrijke basisset voor leerlingen? De kans dat je daarmee expliciet aanstuurt op daling van het niveau lijkt mij groter dan dat het tot een hoger niveau zal leiden.

_____________________________________________________________________________________________________________________________________________________

De kans dat je daarmee expliciet aanstuurt op daling van het niveau lijkt groter dan dat het tot een hoger niveau zal leiden.

______________________________________________________________________________________________________________________________________________________