Curriculumontwikkeling bij wiskunde

Een curriculum opstellen voor wiskunde voor het funderend onderwijs voor een land of deelstaat is een complexe taak. Er zijn tal van bouwstenen beschikbaar, die bovendien op uiteenlopende niveaus van abstractie kunnen worden geformuleerd, aangeboden en getoetst.

In het meest traditionele beeld van wiskundeonderwijs voor de basisschool gaat het slechts om optellen, aftrekken, vermenigvuldigen en delen van verschillende soorten getallen: de Victoriaanse ‘arithmetic’ (3Rs, Reading, ‘Riting, ‘Rithmetic) uit de negentiende eeuw. De bijbehorende procedures op leitje of met pen op papier moesten goed uitgelegd worden en om de procedures (bewerkingen, algoritmen) vlot uit te voeren moest er veel geoefend worden. Het opgedane repertoire vervolgens in de praktijk gebruiken ging niet zomaar vanzelf. In allerlei situaties werden daarvoor tabellenboekjes met de voor die situatie relevante berekeningen gebruikt.

Aan de andere kant van het traditionele spectrum zijn er ook beelden dat wiskunde vooral draait om het manipuleren met abstracte vormen als voorbereiding op de wiskunde en natuurwetenschappen en dat het vak slechts voor een klein gedeelte van de populatie is weggelegd.

De afgelopen decennia is er internationaal veel werk verricht om te definiëren wat mensen in hun dagelijks leven, als burger en als werknemer, daadwerkelijk aan wiskundige kennis en vaardigheden gebruiken. De digitalisering en technologisering van onze samenleving, die voor een groot deel op wiskundige principes rusten, hebben het gebruik van wiskundige representaties verbreed en verdiept.

Wat is zoal terug te vinden aan bouwstenen in actuele wiskundecurricula wereldwijd als gevolg van die ontwikkelingen? Het opbouwen van een basisrepertoire start al in de voorschoolse periode door allerlei ervaringen van jonge kinderen met aantallen en oriëntatie in de ruimte. De school verbindt daar op een geven moment conventies, schrijfwijzen, procedures en nomenclatuur aan zodat wiskunde ook in onderlinge communicatie een gemeenschappelijke taal kan worden.

In eerste instantie speelt dat zich af met eencijferige getallen. Er ontstaat een basisrepertoire. Dat kan overigens nog veel vormen hebben. Sommige curricula leggen daar nog eens een strikte uniformiteit en gestructureerd aanbod in schoolse werkvormen overheen, andere curricula kiezen voor het stimuleren van het interpreteren en herkennen wat het jonge kind in de wereld zoal tegenkomt, bijvoorbeeld door rijke gecijferdheidssituaties te creëren in allerlei spelmomenten. Daarbij kun je denken aan beelden, veel auditief gebruik van aantallen, veel tactiel gebruik van aantallen, gebruik in spelletjes.

Traditioneel volgde dan in hogere groepen heel veel onderwijstijd voor het aanleren van het handmatig uitvoeren van procedures voor grote bewerkingen waarbij algoritmes uitgevoerd dienden te worden met pen op papier. Daar kan tegenwoordig onderwijstijd op bezuinigd worden. Wereldwijd is dit specifieke onderdeel – het uitvoeren van de grote complexe bewerkingen – in het dagelijks handelen inmiddels verdrongen door de rekenmachines, apps en software.

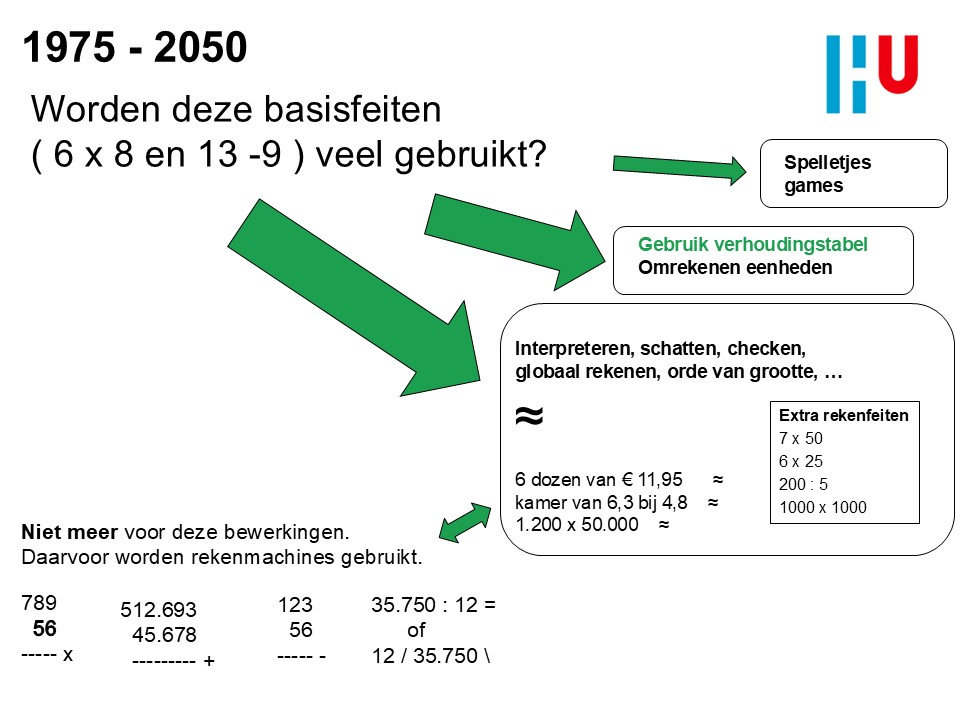
Bij de leerlingen moet dus op een geven moment wel die rekenmachine geïntroduceerd worden én geoefend en herhaald en verrijkt. Want ook goed en verstandig inzetten van een rekenmachine is een vaardigheid.

Steeds vaker staat in moderne curricula een aantal belangrijke wiskundige denk- en handelwijzen centraal: interpreteren, redeneren, abstraheren, mathematiseren, probleemoplossen, modelleren, gebruiken en begrijpen van algoritmisch handelen, kritisch denken, en vergelijkbare hogere orde vaardigheden.

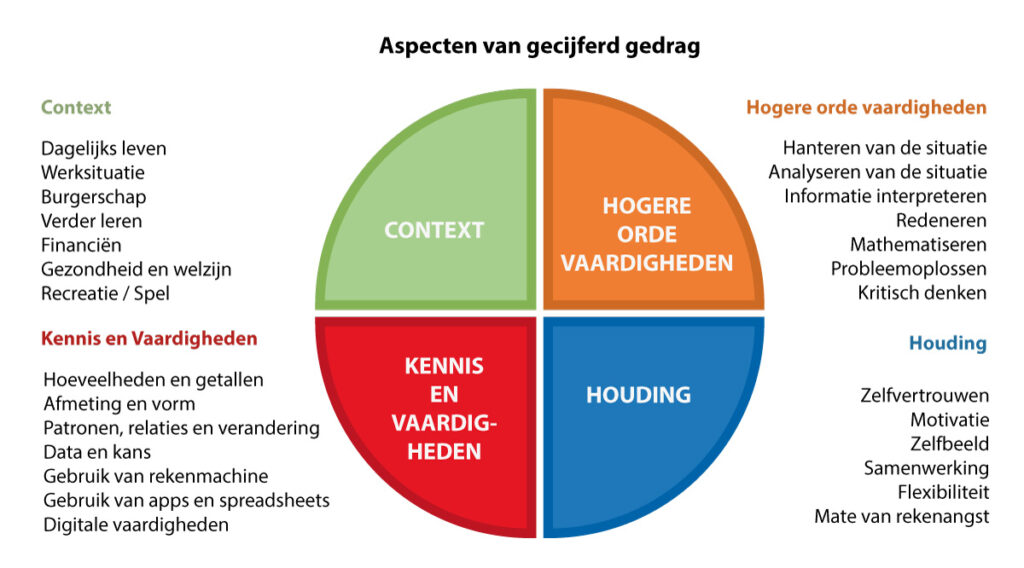
Juist daarin komt het samenhangend werken mét feiten en geleerde procedures, áán oplossingen, ín betekenisvolle situaties bijeen. Daarmee komen leerlingen in de wereld van de wiskunde als model voor de werkelijkheid en pendelen heen en weer tussen wiskundige denk- en handelwijzen en de werkelijkheid. Welke denk- en handelwijzen nu precies gekozen worden is daarbij geen eens zo van belang.

Belangrijke keuzes die gemaakt (moeten) worden zijn verder:

Worden de doelen vooral procedureel ingericht en geïsoleerd onderwezen, geoefend en getoetst. Of worden de doelen behaald door het relevant en adequaat inzetten bij het werken aan de hogere orde doelen in allerlei situaties. Of een mix van beide.
Moeten alle procedurele doelen, ook grote bewerkingen, nog steeds met pen en papier uitgevoerd worden, of wordt er vanaf een bepaalde leeftijd ervoor gekozen om bij grote bewerkingen en complexe breukberekeningen er goede instructie komt over correct en competent gebruik van rekentools.
Hoe abstract worden nieuwe inhouden geïntroduceerd? Altijd startend vanuit abstracte representatie? Of wordt er ook ruimte gelaten voor een concretere niveaus van kennisrepresentatie, zoals in het veelgebruikte handelingsmodel. Niet alle wiskundekennis wordt verworven via een route naar abstractie en terug. Nieuwe wiskundige denk- en handelwijze verwerven via situationele nabijheid komt in de praktijk veel vaker voor: “Wat ik hier moet doen, lijkt erg op …..”
In welke mate wil je werken aan een positieve wiskunde attitude, motivatie, plezier in wiskunde en het tegengaan van rekenangst. Dat vergt namelijk ook tijd en aandacht.
In welke mate wil je het curriculum atomiseren in kleine onderdeeltjes die apart aangeleerd moeten worden. Die neiging is sterk terug te zien in sommige curricula, vaak ook op verzoek van leraren om “precies te weten wat er geleerd moet worden”. Een wens die vaker voorkomt bij een lerarenveld dat wantrouwend is bejegend dooor de wergever en Inspectie en steeds maar louter is afgerekend op toetsresultaten. Of staan er een aantal “big ideas” centraal en komen die in allerlei opdrachten terug en heb je er vertrouwen in dat leerlingen dan ook veel en kennisrijk leren, maar misschien niet allemaal 100% hetzelfde.

De nieuwe Vlaamse minimumdoelen voor wiskunde

Wiskunde is een van de leergebieden in het rapport Kennisrijke minimumdoelen in het Vlaams basisonderwijs.

De inleiding op de nieuwe wiskundedoelen, genaamd “De visie op het vak Wiskunde”, is in grote lijnen conform wat wereldwijde tendensen zijn in de ontwikkeling van modern wiskundeonderwijs. Misschien toont men zich in deze visie meer dan gemiddeld bewust van de eisen die de huidige maatschappij stelt aan het wiskundeonderwijs in de 21^e eeuw door de expliciete verwijzing naar wiskundige geletterdheid en wiskunde in de beroepscontext. De visie sluit ook aan bij de tendensen die geïdentificeerd zijn in het domeinsspecifieke wetenschappelijke onderzoeksveld “mathematics education”.

De visie op het vak Wiskunde

Uit het rapport rond de visie:

DEF_Rapport_Vlaamse_kennisrijke_Minimumdoelen_Bijlage_visie_per_vak Download

Wiskundige geletterdheid omvat de wiskundevaardigheden die nodig zijn om volwaardig te participeren in de samenleving en functionele problemen op te lossen. Het betekent dat iemand de rol van wiskunde in de wereld herkent, begrijpt en toepast om weloverwogen beslissingen te nemen. Wiskundige geletterdheid is essentieel voor kritisch burgerschap en actieve maatschappelijke deelname.

Naast wiskundige geletterdheid vragen veel beroepen om specifieke wiskundige vaardigheden. Een kapper rekent met verhoudingen bij het mengen van haarkleuren, terwijl een bedrijfseconoom wiskundige modellen gebruikt om winstprognoses te maken. Deze toepassingen vragen om inzicht in wiskundige concepten die verder gaan dan wiskundige geletterdheid en afgestemd zijn op de context van het beroep.

Op basis van deze visie is het een prachtige uitdaging om daarbij de juiste wiskundige concepten, denk- en handelwijzen te zoeken en die terug te vertalen naar leerlingen uit groep 6, groep 4 en kleuters: Wat van vroeger is nog wel relevant, wat niet meer? Waar liggen kansen om te komen tot een functioneel repertoire voor een zo groot mogelijke populatie? Waar ligt de prioriteit en wat behoeft echt uitbreiding en nieuwe ontwikkeling en wat wordt een beetje teruggeschroefd? Wordt alles eendimensionaal aangeboden in louter formele wiskundetaal met een gerichtheid op opleveren van juiste antwoorden op sommetje of is er ook ruimte of misschien zelfs wel noodzaak om expliciet aandacht te besteden aan de veelvormigheid waarin de wiskundige informatie tot ons komt. Wat wordt de rol van de alomtegenwoordige rekenmachine? Ook de wiskundige attitude is natuurlijk van belang; welk beeld over wiskunde breng je over op de leerling en met welk beeld over wiskunde wil dat de leerling de school verlaat en het opgedane repertoire gaat gebruiken in vervolgstudies en het dagelijkse leven?

Het is daarmee een grote klus deze visie-elementen te vertalen naar daadwerkelijke onderwijsdoelen en uiteindelijk naar onderwijsmaterialen en -vormen. Daarvoor is veel onderzoek nodig dat analyseert wat de huidige participerende burger en professional nu precies gebruiken in het dagelijks leven. De ingenieur gebruikt tegenwoordig in toenemende mate statistiek in plaats van technische middelen. Stop je dan in het curriculum de meest tijd in procedureel manipuleren met cijfers en later letters (algebra) of zet je ‘data science’ veel centraler? Steeds vaker is informatie die tot ons komt gegoten in een wiskundige representatie: getallen, tabellen, grafieken, …… Hoe bereid je leerlingen daar nu op voor?

De uitwerking in de minimumdoelen

Wetenschappelijke onderbouwing

Een serieus probleem in deze uitwerking is de keuze van wetenschappelijke onderbouwing. Er is de laatste 70 jaar een zeer omvangrijk corpus aan theorie en wetenschappelijke resultaten opgebouwd in het domeinspecifieke wetenschapsdomein “Mathematics Education”, dat wereldwijd gezien wordt als een erkend zelfstandig onderzoeksgebied. De conferenties ICME (4 jaarlijks wereldwijd, meer dan 100 landen), CERME (2 jaarlijks, vooral Europees) en PME (jaarlijks, wereldwijd) zijn daarin conceptueel toonaangevend. Vanuit die wetenschappelijke kennisbasis wordt over het algemeen een breder, meer holistisch en meer multidisciplinair perspectief geboden op de cognitieve schema’s die leerlingen ontwikkelen op het gebied van rekenen-wiskunde en waar ze in hun verder schoolloopbaan gebruik van maken (wiskunde, statistiek), maar zeker ook in het dagelijkse leven (gecijferdheid). Die denkschema’s zijn ook nodig om volwaardig te kunnen participeren in onze steeds verder “mathematiserende” samenleving. De verworven inzichten uit dit domeinspecifieke corpus ontbreken vrijwel geheel in de uitwerking. De gemaakte keuzes lijken eerder ideologisch dan wetenschappelijk geïnspireerd, met een opvallende verwijzing naar de “cultural literacy” visie van E.D. Hirsch jr.. Hirsch heeft echter nooit onderbouwd iets geschreven over het leren van wiskunde, hooguit in clichématige bewoordingen. Dat curriculummakers hun keuzes voor het verwerven van wiskundekennis voor het hele funderend onderwijs mogelijk baseren op redelijk simplistische, bijna behavioristische, opvattingen over het verwerven van – grotendeels trivia – kennis, zou echt schadelijk kunnen uitpakken voor de benodigde gelaagdheid in de wiskundige ontwikkeling van de leerlingen, zoals het in samenhang wiskundefeiten, procedures, tools en wiskundige denk- en handelwijzen gebruiken om problemen in je eigen dagelijkse leven aan te pakken.

Empirische onderbouwing

Door de veelheid van keuzes in de uitwerking van een visie tot een curriculum is het van het grootste belang dat gemaakte keuzes uitvoerig worden beproefd op onderwijsbaarheid door leraren en leerbaarheid door de beoogde leeftijdsgroep. Zonder dat is implementatie een blinde en mijns inziens onverantwoordelijke gok. Het is een politiek risico voor de bewindspersonen en een inhoudelijk risico voor de curriculummakers om zonder beproeving door ervaren leraren hun keuzes te vast te leggen vanuit een zeer beperkt perspectief, zoals de ideeën van de inmiddels bijna 100-jarige E.D. Hirsch jr. over wat relevante kennis is voor de toekomstige generaties leerlingen.

Overladenheid

Als je wereldwijd analyseert welk wiskundig repertoire er beoogd en bereikt wordt voor diverse leeftijdsgroepen, dan zie je een zekere bandbreedte per leeftijdsgroep — maar geen extreme uitschieters naar boven of beneden, zelfs niet in laag of hoog scorende landen. Ook daar zijn voor elke leeftijdsgroep een redelijke set van vrij gangbare, moderne doelen astgesteld. De mate waarin die doelen slecht of goed worden behaald, hangen meestal samen met heersende economische factoren.

In dit curriculumvoorstel zie ik -daarmee vergeleken – te veel, te abstract aangevlogen, losse onderwerpen met nauwelijks tot geen ruimte voor werken aan samenhang. Veel onderwerpen komen volgens mij ook veel te vroeg voor de leerlingpopulatie met daarbij onrealistische haalpercentages als: ” gehele populatie”. Leerlingen in groep 6 moeten 258 specifieke doelen hebben gehaald, met daarbij nog enkele tientallen subdoelen. Bij elkaar zo’n 300 doelen. In 6 jaar tijd zijn er waarschijnlijk zo’n 900 lessen wiskunde in de basisschool. Niet alle doelen zijn natuurlijk even omvangrijk, maar het geeft wel een indicatie hoeveel tijd er gemiddeld is om een doel te bereiken in de geven lessen , ik denk zo’n 1 á 3 lessen. Zo’n doel is dan bijvoorbeeld voor groep 4:

2.2.14 De leerlingen kunnen flexibel een doelmatige rekenmethode uitkiezen, uitvoeren en verantwoorden op basis van inzicht in de getalstructuur en begrip van de rekenhandelingen. Keuze uit: ● hoofdrekenen: standaardprocedures; ● hoofdrekenen: handig rekenen, meer bepaald compenseren en eigenschappen van bewerkingen gebruiken.

Mijn conclusie: in plaatst van scherpe keuzes gericht op de huidige en toekomstige tijd lijkt het vooral of alles is behouden: wat vroeger van belang was (en mogelijk nu niet meer), wat nu praktijk in scholen is en een klein beetje wat er voor de toekomst nodig is.

De atomisering van het curriculum

Het grootste deel van de doelen is gedetailleerde wiskundige kennis en conventies, abstract geformuleerd en heel veel procedures. Er is relatief heel weinig aandacht voor samenhang, waardoor het curriculum sterk versnipperd oogt. Het is een voorbeeld van een geatomiseerd curriculum, waarbij vermoedelijk de achterliggende gedachte is dat je daarmee helder bent wat er precies geleerd moet worden.

Het gebrek aan hogere orde vaardigheden

Het toevoegen van hogere orde vaardigheden waarin al die rekenkennis en de procedures doelgericht gebruikt zouden kunnen worden blijft beperkt tot ‘probleemoplossen’ en ‘grote vraagstukken’ en beslaat precies 5 van de 258 hoofddoelen. Dat is een duidelijk signaal vanuit de curriculummakers aan de leraren en methodeschrijvers dat daar niet de essentie of de hoofdmoot of het uitgangspunt van het curriculum ligt. De sterke nadruk ligt op de losse atomen en daarmee op het reproduceren van geïsoleerde kennisfeiten en het oefenen van vaardigheden los van relevant gebruik.

Eruditie op het verkeerde spoor

En dan is nog de vraag op welke leeftijd het realistisch is wat te kunnen bereiken en voor welk gedeelte van de populatie. Het voorstel is doorgeschoten in procedurele fixatie en abstracte eruditie.

Hoge verwachtingen hebben is niet hetzelfde als onrealistische eisen stellen.

Grote ambitie heben is wat anders dan de leerstof op hoog abstractieniveau aanvliegen. Hoge ambitie kan ook zijn of juist zoveel mogelijk leerlingen inclusief meenemen, ook leerlingen die soms verschillende benaderingen behoeven of vanuit een geheel andere kennisbasis starten.

Het maakt veel verschil voor het werken in de klas bij hoeveel leerlingen je kunt werken in hun zone van naaste ontwikkeling of dat leerlingen heel vaak zullen worden verbannen naar hun zone van discomfort, hetgeen grote uitval en rekenangst zal genereren.

Kennisrijk

Kennisrijk is niet hetzelfde als snel abstraheren en formaliseren en dan alles formeel aanbieden. Dat staat bekend als de zogenaamde high-level-illusion: oogt indrukwekkend erudiet, maar zal vervallen voor het merendeel in eindeloos trainen op specifieke trucjes bij elk doel.

Hoog niveau bij wiskundeonderwijs wordt voornamelijk behaald door de mate waarin de genoemde hogere orde doelen worden bereikt. Daarbij gaat het om wiskundige denk- en handelwijzen en niet om culturele trivia.

Het is niet makkelijk om les te geven in wiskundige denk- en handelwijzen, niet makkelijk om te vertalen naar alle niveaus leerlingen, niet makkelijk te toetsen, maar wel de pedagogische en educatieve opdracht van deze tijd: ook leerlingen voor wie het leren niet makkelijk gaat, hebben salaris, gaan huizen huren, gebruiken medicijnrecepten, lezen getallen in de media, en wiskunde helpt hen daarbij om kwalitatief goed te participeren.

Verwachte uitwerking in de praktijk

Er is redelijk veel bekend over de gevolgen van een overlade, te abstract aangevlogen en geatomiseerd wiskundecurriculum. In de praktijk zullen methodenmakers, leraren en toetsmakers door de overladenheid en atomisering alle doelen proberen te vertalen in eenvoudig reproduceerbare opgaven of sommetjes. Voor de vorm zal aan het eind van een hoofdstuk ook nog een aantal toepassingen met probleemoplossen worden opgenomen, mogelijk zelfs niet meer dan een aantal redactiesommen.

Door de druk van de overladenheid zullen heel veel leraren ook in de klas doelen gaan reduceren tot lagere orde reproductiedoelen, zodat ze in ieder geval “behandeld” zijn doordat ze ” direct” geïnstrueerd zijn aan de klas. Elke doelzin moet dan in 1 a 2 lessen afgevinkt kunnen worden.

Er zal geen ruimte gevoeld worden om aan de slag te gaan met grotere samenhangende opdrachten waarin juist de wiskundige denk- en handelwijzen centraal staan. Na enkele jaren kan dan het spel weer beginnen wie de “schuld” heeft aan het feit dat dat deze onderwijspraktijken op internationale – meer op samenhang gerichte assessments als PISA – tot slechte scores leidt.

Het geïsoleerd doorwerken van geatomiseerde doelen en mogelijk een fixatie op formele procedures uitvoeren (op werkbladen ??) zal een steeds grotere discrepantie geven met wat leerlingen in de wereld buiten school ervaren wat anderen en zijzelf daadwerkelijk doen aan wiskundige denk- en handelwijzen. Dat zal grote weerslag hebben op de perceptie van het nut van het schoolvak wiskunde en daardoor op de motivatie daarvoor.

Mijn grootste zorg gaat uit naar sociaal kwetsbare groepen leerlingen en leerlingen bij wie het leren moeizaam gaat bij zo’n overladen en te abstract en procedureel programma. Grotere sociale ongelijkheid is eigenlijk overal ter wereld de uitkomst bij dergelijke in ambitie doorgeschoten curricula. Maar het is uiteindelijk een politieke keuze of kwetsbare leerlingen meer steun nodig hebben om de doelen te halen of dat iedereen “gelijke” kansen moet krijgen via een uniform programma.

Ten slotte

Overvolle curricula als deze zie je eerder bij landen die zijn blijven gangen in het verleden en moeilijk in staat zijn hun wiskundecurriculum te actualiseren en moderniseren, vaak om politieke sentimentsredenen of door gebrek aan sterke traditie in domeinspecifiek wiskundedidactisch onderzoek of door een gebrek aan adequaat opgeleide leraren die brede doelen ook bij wiskundeonderwijs handen en voeten kunnen geven. Hier is de TIMSS 2023 lijst te vinden. Denk dan aan landen als Spanje, Portugal, Griekenland, Polen, .. Het zou bijzonder zijn als een land of deelstaat dat ambitieus het curriculum wil verbeteren zich juist in die richting gaat begeven.

Misschien toch wel een gevalletje van ‘hubris’ om in enkele maanden zonder serieuze beproeving in de praktijk een wiskundecurriculum in elkaar te knutselen op basis van een algemene cultuurtheorie uit de vorige eeuw die niet veel verder gaat dan het promoten van uniforme “cultural literacy”.

Deze kritische beschouwing is geschreven op persoonlijke titel.